The maths behind

Imagine having to draw a line passing through a single point, there is an infinite number of possibilities. However, if two different points are required, one and only one line is now possible. This very simple idea is at the heart of Shamir's secret sharing and Lagrange's interpolation around which Qasmat is built.

The line is replaced by a polynomial of degree k-1 whose value at zero is the secret to be protected and other coefficients are chosen at random. Then at least k distinct points of this polynomial are distributed on distant servers.

To recover the secret, at least k points of the polynomial are retrieved from different servers and the polynomial is constructed with Lagrange's interpolation (visualize here). P(0) corresponding to the secret is then computed.

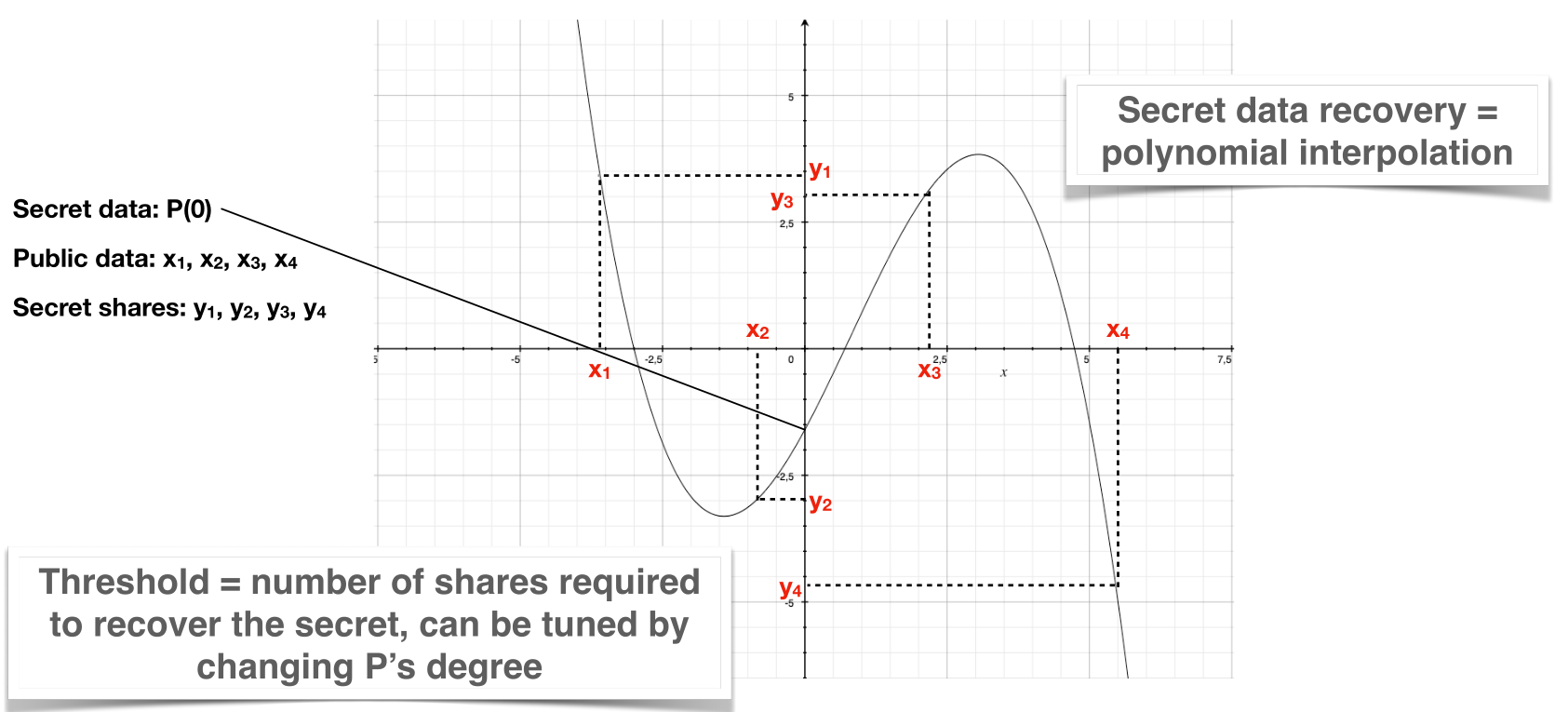
The number of points distributed (n) must be greater than k. Those two values constitute a threshold (k,n) whose value is determined according to the required security (see Security at rest).

Since the coefficients are integers, everything is modular. The modulus is a prime number which avoids basic attacks.